Robustness of critical U(1) spin liquids and emergent symmetries in tensor networks
H. Dreyer, L. Vanderstraeten, J. Y. Chen, R. Verresen, N. Schuch
Physical Review B 109 (19), 195161 (2024).
We study the response of critical resonating valence bond (RVB) spin liquids to doping with longer -range singlets, and more generally of U(1) -symmetric tensor networks to nonsymmetric perturbations. Using a field theory description, we find that in the RVB, doping constitutes a relevant perturbation that immediately opens up a gap, contrary to previous observations. Our analysis predicts a very large correlation length even at significant doping, which we verify using high -accuracy numerical simulations. This emphasizes the need for careful analysis, but it also justifies the use of such states as a variational ansatz for critical systems. Finally, we give an example of a projected entangled pair state where nonsymmetric perturbations do not open up a gap and the U(1) symmetry reemerges.

Symmetry Protected Topological Order in Open Quantum Systems
C. de Groot, A. Turzillo, N. Schuch
Quantum 6, 1-39 (2022).
"We systematically investigate the robustness of symmetry protected topological (SPT) order in open quantum systems by studying the evolution of string order parameters and other probes under noisy channels. We find that one-dimensional SPT order is robust against noisy couplings to the environment that satisfy a strong sym-metry condition, while it is destabilized by noise that satisfies only a weak symmetry condition, which generalizes the notion of symmetry for closed systems. We also discuss ""transmutation "" of SPT phases into other SPT phases of equal or lesser complexity, under noisy channels that satisfy twisted versions of the strong symmetry condition."

Tensor Networks Can Resolve Fermi Surfaces
Q. Mortier, N. Schuch, F. Verstraete, J. Haegeman
Physical Review Letters 129 (20), 206401 (2022).
We demonstrate that projected entangled-pair states are able to represent ground states of critical, fermionic systems exhibiting both 1d and 0d Fermi surfaces on a 2D lattice with an efficient scaling of the bond dimension. Extrapolating finite size results for the Gaussian restriction of fermionic projected entangled-pair states to the thermodynamic limit, the energy precision as a function of the bond dimension is found to improve as a power law, illustrating that an arbitrary precision can be obtained by increasing the bond dimension in a controlled manner. In this process, boundary conditions and system sizes have to be chosen carefully so that nonanalyticities of the Ansatz, rooted in its nontrivial topology, are avoided.

Locality optimization for parent Hamiltonians of tensor networks
G. Giudici, J. I. Cirac, N. Schuch
Physical Review B 106 (3), 35109 (2022).
Tensor network states form a powerful framework for both the analytical and numerical study of strongly correlated phases. Vital to their analytical utility is that they appear as the exact ground states of associated parent Hamiltonians, where canonical proof techniques guarantee a controlled ground space structure. Yet, while those Hamiltonians are local by construction, the known techniques often yield complex Hamiltonians which act on a rather large number of spins. In this paper, we present an algorithm to systematically simplify parent Hamiltonians, breaking them down into any given basis of elementary interaction terms. The underlying optimization problem is a semidefinite program, and thus the optimal solution can be found efficiently. Our method exploits a degree of freedom in the construction of parent Hamiltonians???the excitation spectrum of the local terms???over which it optimizes such as to obtain the best possible approximation. We benchmark our method on the AKLT model and the toric code model, where we show that the canonical parent Hamiltonians (acting on 3 or 4 and 12 sites, respectively) can be broken down to the known optimal two-body and four-body terms. We then apply our method to the paradigmatic resonating valence bond (RVB) model on the kagome lattice. Here, the simplest previously known parent Hamiltonian acts on all the 12 spins on one kagome star. With our optimization algorithm, we obtain a vastly simpler Hamiltonian: we find that the RVB model is the ground state of a parent Hamiltonian whose terms are all products of at most four Heisenberg interactions, and whose range can be further constrained, providing a major improvement over the previously known 12-body Hamiltonian.

Preparation and verification of tensor network states
E. Cruz, F. Baccari, J. Tura, N. Schuch, J. I. Cirac
Physical Review Research 4 (2), 23161 (2022).
We consider a family of tensor network states defined on regular lattices that come with a natural definition of an adiabatic path to prepare them. This family comprises relevant classes of states, such as injective matrix product and projected entangled-pair states, and some corresponding to classical spin models. We show how uniform lower bounds to the gap of the parent Hamiltonian along the adiabatic trajectory can be efficiently computed using semidefinite programming. This allows one to check whether the adiabatic preparation can be performed efficiently with a scalable effort. We also derive a set of observables whose expectation values can be easily determined and that form a complete set, in the sense that they uniquely characterize the state. We identify a subset of those observables which can be efficiently computed if one has access to the quantum state and local measurements, and analyze how they can be used in verification procedures.

On the stability of topological order in tensor network states
D. J. Williamson, C. Delcamp, F. Verstraete, N. Schuch
Physical Review B 104 (23), 235151 (2021).
We construct a tensor network representation of the three-dimensional (3D) toric code ground state that is stable to a generating set of uniform local tensor perturbations, including those that do not map to local operators on the physical Hilbert space. The stability is established by mapping the phase diagram of the perturbed tensor network to that of the 3D Ising gauge theory, which has a nonzero finite temperature transition. More generally, we find that the stability of a topological tensor network state is determined by the form of its virtual symmetries and the topological excitations created by virtual operators that break those symmetries. In particular, a dual representation of the 3D toric code ground state, as well as representations of the X-cube and cubic code ground states, for which pointlike excitations are created by such operators, are found to be unstable.

On tensor network representations of the (3+1)d toric code
C. Delcamp, N. Schuch
Quantum 5, 1-31 (2021).
We define two dual tensor network representations of the (3+1)d toric code ground state subspace. These two representations, which are obtained by initially imposing either family of stabilizer constraints, are characterized by different virtual symmetries generated by string-like and membrane-like operators, respectively. We discuss the topological properties of the model from the point of view of these virtual symmetries, emphasizing the differences between both representations. In particular, we argue that, depending on the representation, the phase diagram of boundary entanglement degrees of freedom is naturally associated with that of a (2+1)d Hamiltonian displaying either a global or a gauge Z(2)-symmetry.

Matrix product states and projected entangled pair states: Concepts, symmetries, theorems
J. I. Cirac, D. Perez-Garcia, N. Schuch, F. Verstraete
Reviews of Modern Physics 93 (4), 45003 (2021).
The theory of entanglement provides a fundamentally new language for describing interactions and correlations in many-body systems. Its vocabulary consists of qubits and entangled pairs, and the syntax is provided by tensor networks. How matrix product states and projected entangled pair states describe many-body wave functions in terms of local tensors is reviewed. These tensors express how the entanglement is routed, act as a novel type of nonlocal order parameter, and the manner in which their symmetries are reflections of the global entanglement patterns in the full system is described. The manner in which tensor networks enable the construction of real-space renormalization group flows and fixed points is discussed, and the entanglement structure of states exhibiting topological quantum order is examined. Finally, a summary of the mathematical results of matrix product states and projected entangled pair states, highlighting the fundamental theorem of matrix product vectors and its applications, is provided.

Entanglement Order Parameters and Critical Behavior for Topological Phase Transitions and Beyond
M. Iqbal, N. Schuch
Physical Review X 11 (4), 41014 (2021).
Order parameters are key to our understanding of phases of matter. Not only do they allow one to classify phases, but they also enable the study of phase transitions through their critical exponents which identify the universal long-range physics underlying the transition. Topological phases are exotic quantum phases which are lacking the characterization in terms of order parameters. While probes have been developed to identify such phases, those probes are only qualitative, in that they take discrete values, and, thus, provide no means to study the scaling behavior in the vicinity of phase transitions. In this paper, we develop a unified framework based on variational tensor networks (infinite projected entangled pair states) for the quantitative study of both topological and conventional phase transitions through entanglement order parameters. To this end, we employ tensor networks with suitable physical and/or entanglement symmetries encoded and allow for order parameters detecting the behavior of any of those symmetries, both physical and entanglement ones. On the one hand, this gives rise to entanglement-based order parameters for topologically ordered phases. These topological order parameters allow one to quantitatively probe the behavior when going through topological phase transitions and, thus, to identify universal signatures of such transitions. We apply our framework to the study of the toric code model in different magnetic fields, which along some special lines maps to the (2 + 1) Ising model. Our method identifies 3D Ising critical exponents for the entire transition, consistent with those special cases and general belief. However, we, in addition, also find an unknown critical exponent beta* approximate to 0.021 for one of our topological order parameters. We take this-together with known dualities between the toric code and the Ising model-as a motivation to also apply our framework of entanglement order parameters to conventional phase transitions. There, it enables us to construct a novel type of disorder operator (or disorder parameter), which is nonzero in the disordered phase and measures the response of the wave function to a symmetry twist in the entanglement. We numerically evaluate this disorder operator for the (2 + 1) transverse field Ising model, where we again recover a critical exponent hitherto unknown in the (2 + 1) Ising model, beta* approximate to 0.024, consistent with the findings for the toric code. This shows that entanglement order parameters can provide additional means of characterizing the universal data both at topological and conventional phase transitions and altogether demonstrates the power of this framework to identify the universal data underlying the transition.

Generating function for tensor network diagrammatic summation
W. L. Tu, H. K. Wu, N. Schuch, N. Kawashima, J. Y. Chen
Physical Review B 103 (20), 205155 (2021).
The understanding of complex quantum many-body systems has been vastly boosted by tensor network (TN) methods. Among others, excitation spectrum and long-range interacting systems can be studied using TNs, where one however confronts the intricate summation over an extensive number of tensor diagrams. Here, we introduce a set of generating functions, which encode the diagrammatic summations as leading-order series expansion coefficients. Combined with automatic differentiation, the generating function allows us to solve the problem of TN diagrammatic summation. We illustrate this scheme by computing variational excited states and the dynamical structure factor of a quantum spin chain, and further investigating entanglement properties of excited states. Extensions to infinite-size systems and higher dimension are outlined.

Fractional chiral hinge insulator
A. Hackenbroich, A. Hudomal, N. Schuch, B. A. Bernevig, N. Regnault
Physical Review B 103 (16), L161110 (2021).
We propose and study a wave function describing an interacting three-dimensional fractional chiral hinge insulator (FCHI) constructed by Gutzwiller projection of two noninteracting second-order topological insulators with chiral hinge modes at half filling. We use large-scale variational Monte Carlo computations to characterize the model states via the entanglement entropy and charge-spin fluctuations. We show that the FCHI possesses fractional chiral hinge modes characterized by a central charge c = 1 and Luttinger parameter K = 1/2, like the edge modes of a Laughlin 1/2 state. The bulk and surface topology is characterized by the topological entanglement entropy (TEE) correction to the area law. While our computations indicate a vanishing bulk TEE, we show that the gapped surfaces host an unconventional two-dimensional topological phase. In a clear departure from the physics of a Laughlin 1/2 state, we find a TEE per surface compatible with (In root 2)/2, half that of a Laughlin 1/2 state. This value cannot be obtained from topological quantum field theory for purely two-dimensional systems. For the sake of completeness, we also investigate the topological degeneracy.

Projected Entangled Pair States: Fundamental Analytical and Numerical Limitations
G. Scarpa, A. Molnar, Y. Ge, J. J. Garcia-Ripoll, N. Schuch, D. Perez-Garcia, S. Iblisdir
Physical Review Letters 125 (21), 210504 (2020).
Matrix product states and projected entangled pair states (PEPS) are powerful analytical and numerical tools to assess quantum many-body systems in one and higher dimensions, respectively. While matrix product states are comprehensively understood, in PEPS fundamental questions, relevant analytically as well as numerically, remain open, such as how to encode symmetries in full generality, or how to stabilize numerical methods using canonical forms. Here, we show that these key problems, as well as a number of related questions, are algorithmically undecidable, that is, they cannot be fully resolved in a systematic way. Our work thereby exposes fundamental limitations to a full and unbiased understanding of quantum many-body systems using PEPS.

Quantum trimer models and topological SU(3) spin liquids on the kagome lattice
S. Jandura, M. Iqbal, N. Schuch
Physical Review Research 2 (3), 33382 (2020).
We construct and study quantum trimer models and resonating SU(3)-singlet models on the kagome lattice, which generalize quantum dimer models and the resonating valence bond wave functions to a trimer and SU(3) setting. We demonstrate that these models carry a Z(3) symmetry which originates in the structure of trimers and the SU(3) representation theory, and which becomes the only symmetry under renormalization. Based on this, we construct simple and exact parent Hamiltonians for the model which exhibit a topological ninefold degenerate ground space. A combination of analytical reasoning and numerical analysis reveals that the quantum order ultimately displayed by the model depends on the relative weight assigned to different types of trimers-it can display either Z(3) topological order or form a symmetry-broken trimer crystal, and in addition possesses a point with an enhanced U(1) symmetry and critical behavior. Our results accordingly hold for the SU(3) model, where the two natural choices for trimer weights give rise to either a topological spin liquid or a system with symmetry-broken order, respectively. Our work thus demonstrates the suitability of resonating trimer and SU(3)-singlet ansatzes to model SU(3) topological spin liquids on the kagome lattice.

Efficient Description of Many-Body Systems with Matrix Product Density Operators
J. G. Jarkovsky, A. Molnar, N. Schuch, J. I. Cirac
Prx Quantum 1 (1), 10304 (2020).
"Matrix product states form a powerful ansatz for the simulation of a wide range of one-dimensional quantum systems that are in a pure state. Their power stems from the fact that they faithfully approximate states with a low amount of entanglement, the ""area law."" However, in order to accurately capture the physics of realistic systems, one generally needs to apply a mixed-state description. In this work, we establish the mixed-state analog of this characterization. We show that one-dimensional mixed states with a low amount of entanglement, quantified by the entanglement of purification, can be efficiently approximated by matrix product density operators."

Resolving Fermi surfaces with tensor networks
Q. Mortier, N. Schuch, F. Verstraete, J. Haegeman
We show that Projected Entangled-Pair States (PEPS) are able to describe critical, fermionic systems exhibiting both 1d and 0d Fermi surfaces on a 2d lattice. In the thermodynamic limit, the energy precision as a function of the bond dimension improves as a power law, illustrating that an arbitrary precision can be obtained by increasing the bond dimension in a controlled manner. We also identify a non-trivial obstruction in the Gaussian and fermionic variant of PEPS, rooted in its topology and restricting its efficient applicability to models with a matching parity configuration.

Inaccessible entanglement in symmetry protected topological phases
C. de Groot, D. T. Stephen, A. Molnar, N. Schuch
Journal of Physics a-Mathematical and Theoretical 53 (33), 335302 (2020).
We study the entanglement structure of symmetry-protected topological (SPT) phases from an operational point of view by considering entanglement distillation in the presence of symmetries. We demonstrate that non-trivial SPT phases in one-dimension necessarily contain some entanglement which is inaccessible if the symmetry is enforced. More precisely, we consider the setting of local operations and classical communication (LOCC) where the local operations commute with a global onsite symmetry groupG, which we callG-LOCC, and we define the inaccessible entanglement E(inacc)as the entanglement that cannot be used for distillation underG-LOCC. We derive a tight bound on E(inacc)which demonstrates a direct relation between inaccessible entanglement and the SPT phase, namely log(D-omega(2)) <= E-inacc <= log(vertical bar G vertical bar), whereD(omega)is the topologically protected edge mode degeneracy of the SPT phase omega with symmetryG. For particular phases such as the Haldane phase,D omega = root|G| so the bound becomes an equality. We numerically investigate the distribution of states throughout the bound, and show that typically the region near the upper bound is highly populated, and also determine the nature of those states lying on the upper and lower bounds. We then discuss the relation of E-inacc to string order parameters, and also the extent to which it can be used to distinguish different SPT phases of matter.

SU(3)(1) Chiral Spin Liquid on the Square Lattice: A View from Symmetric Projected Entangled Pair States
J. Y. Chen, S. Capponi, A. Wietek, M. Mambrini, N. Schuch, D. Poilblanc
Physical Review Letters 125 (1), 17201 (2020).
Quantum spin liquids can be faithfully represented and efficiently characterized within the framework of projected entangled pair states (PEPS). Guided by extensive exact diagonalization and density matrix renormalization group calculations, we construct an optimized symmetric PEPS for a SU(3)(1) chiral spin liquid on the square lattice. Characteristic features are revealed by the entanglement spectrum (ES) on an infinitely long cylinder. In all three Z(3) sectors, the level counting of the linear dispersing modes is in full agreement with SU(3)(1) Wess-Zumino-Witten conformal field theory prediction. Special features in the ES are shown to be in correspondence with bulk anyonic correlations, indicating a fine structure in the holographic bulk-edge correspondence. Possible universal properties of topological SU(N)(k) chiral PEPS are discussed.

Gapped Z(2) spin liquid in the breathing kagome Heisenberg antiferromagnet
M. Iqbal, D. Poilblanc, N. Schuch
Physical Review B 101 (15), 155141 (2020).
We investigate the spin-1/2 Heisenberg antiferromagnet on a kagome lattice with breathing anisotropy (i.e., with weak and strong triangular units), constructing an improved simplex resonating valence bond (RVB) ansatz by successive applications (up to three times) of local quantum gates, which implement a filtering operation on the bare nearest-neighbor RVB state. The resulting projected entangled pair state involves a small number of variational parameters (only one at each level of application) and preserves full lattice and spin-rotation symmetries. Despite its simple analytic form, the simplex RVB provides very good variational energies at strong and even intermediate breathing anisotropy. We show that it carries Z(2) topological order which does not fade away under the first few applications of the quantum gates, suggesting that the RVB topological spin liquid becomes a competing ground state candidate for the kagome antiferromagnet at large breathing anisotropy.

Fermionic tensor networks for higher-order topological insulators from charge pumping
A. Hackenbroich, B. A. Bernevig, N. Schuch, N. Regnault
Physical Review B 101 (11), 115134 (2020).
We apply the charge-pumping argument to fermionic tensor network representations of d-dimensional topological insulators (TIs) to obtain tensor network states (TNSs) for (d + 1)-dimensional TIs. We exemplify the method by constructing a two-dimensional projected entangled pair state (PEPS) for a Chern insulator starting from a matrix product state (MPS) in d = 1 describing pumping in the Su-Schrieffer-Heeger (SSH) model. In extending the argument to second-order TIs, we build a three-dimensional TNS for a chiral hinge TI from a PEPS in d = 2 for the obstructed atomic insulator (OAI) of the quadrupole model. The (d + 1)dimensional TNSs obtained in this way have a constant bond dimension inherited from the d-dimensional TNSs in all but one spatial direction, making them candidates for numerical applications. From the d-dimensional models, we identify gapped next-nearest-neighbor Hamiltonians interpolating between the trivial and OAI phases of the fully dimerized SSH and quadrupole models, whose ground states are given by an MPS and a PEPS with a constant bond dimension equal to 2, respectively.

Classification of Matrix-Product Unitaries with Symmetries
Z. P. Gong, C. Sunderhauf, N. Schuch, J. I. Cirac
Physical Review Letters 124 (10), 100402 (2020).
We prove that matrix-product unitaries with on-site unitary symmetries are completely classified by the (chiral) index and the cohomology class of the symmetry group G, provided that we can add trivial and symmetric ancillas with arbitrary on-site representations of G. If the representations in both system and ancillas are fixed to be the same, we can define symmetry-protected indices (SPIs) which quantify the imbalance in the transport associated to each group element and greatly refines the classification. These SPIs are stable against disorder and measurable in interferometric experiments. Our results lead to a systematic construction of two-dimensional Floquet symmetry-protected topological phases beyond the standard classification, and thus shed new light on understanding nonequilibrium phases of quantum matter.

Topological spin liquids: Robustness under perturbations
M. Iqbal, H. Casademunt, N. Schuch
Physical Review B 101 (11), 115101 (2020).
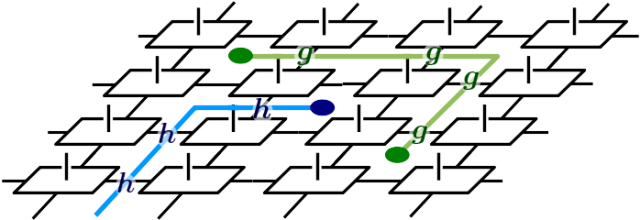
We study the robustness of the paradigmatic kagome resonating valence bond (RVB) spin liquid and its orthogonal version, the quantum dimer model. The nonorthogonality of singlets in the RVB model and the induced finite length scale not only makes it difficult to analyze, but can also significantly affect its physics, such as how much noise resilience it exhibits. Surprisingly, we find that this is not the case: The amount of perturbations which the RVB spin liquid can tolerate is not affected by the finite correlation length, making the dimer model a viable model for studying RVB physics under perturbations. Remarkably, we find that this is a universal phenomenon protected by symmetries: First, the dominant correlations in the RVB are spinon correlations, making the state robust against doping with visons. Second, reflection symmetry stabilizes the spin liquid against doping with spinons, by forbidding mixing of the initially dominant correlations with those which lead to the breakdown of topological order.

Matrix product state algorithms for Gaussian fermionic states
N. Schuch, B. Bauer
Physical Review B 100 (24), 245121 (2019).
While general quantum many-body systems require exponential resources to be simulated on a classical computer, systems of noninteracting fermions can be simulated exactly using polynomially scaling resources. Such systems may be of interest in their own right but also occur as effective models in numerical methods for interacting systems, such as Hartree-Fock, density functional theory, and many others. Often it is desirable to solve systems of many thousand constituent particles, rendering these simulations computationally costly despite their polynomial scaling. We demonstrate how this scaling can be improved by adapting methods based on matrix product states, which have been enormously successful for low-dimensional interacting quantum systems, to the case of free fermions. Compared to the case of interacting systems, our methods achieve an exponential speedup in the entanglement entropy of the state. We demonstrate their use to solve systems of up to one million sites with an effective matrix product state bond dimension of 10(15).

Quantum chaos in the Brownian SYK model with large finite N : OTOCs and tripartite information
C. Sunderhauf, L. Piroli, X. L. Qi, N. Schuch, J. I. Cirac
Journal of High Energy Physics 2019, 38 (2019).
We consider the Brownian SYK model of N interacting Majorana fermions, with random couplings that are taken to vary independently at each time. We study the out-of-time-ordered correlators (OTOCs) of arbitrary observables and the Renyi-2 tripartite information of the unitary evolution operator, which were proposed as diagnostic tools for quantum chaos and scrambling, respectively. We show that their averaged dynamics can be studied as a quench problem at imaginary times in a model of N qudits, where the Hamiltonian displays site-permutational symmetry. By exploiting a description in terms of bosonic collective modes, we show that for the quantities of interest the dynamics takes place in a subspace of the effective Hilbert space whose dimension grows either linearly or quadratically with N , allowing us to perform numerically exact calculations up to N = 10(6). We analyze in detail the interesting features of the OTOCs, including their dependence on the chosen observables, and of the tripartite information. We observe explicitly the emergence of a scrambling time t* similar to ln N controlling the onset of both chaotic and scrambling behavior, after which we characterize the exponential decay of the quantities of interest to the corresponding Haar scrambled values.

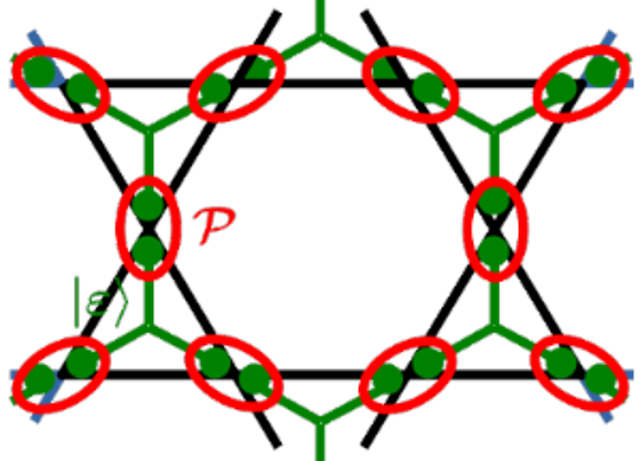
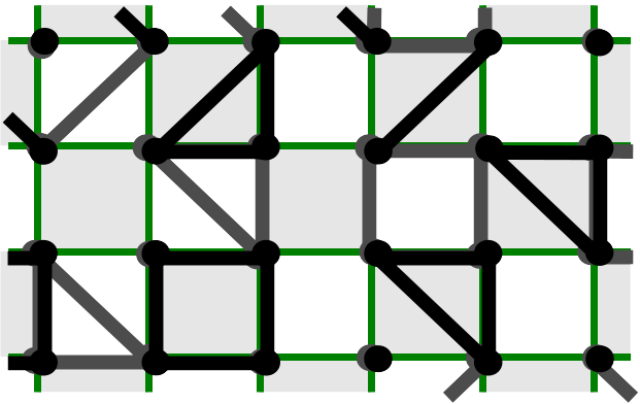
Detecting subsystem symmetry protected topological order via entanglement entropy
D. T. Stephen, H. Dreyer, M. Iqbal, N. Schuch
Physical Review B 100 (11), 115112 (2019).
Subsystem symmetry protected topological (SSPT) order is a type of quantum order that is protected by symmetries acting on lower-dimensional subsystems of the entire system. In this paper, we show how SSPT order can be characterized and detected by a constant correction to the entanglement area law, similar to the topological entanglement entropy. Focusing on the paradigmatic two-dimensional cluster phase as an example, we use tensor network methods to give an analytic argument that almost all states in the phase exhibit the same correction to the area law, such that this correction may be used to reliably detect the SSPT order of the cluster phase. Based on this idea, we formulate a numerical method that uses tensor networks to extract this correction from ground-state wave functions. We use this method to study the fate of the SSPT order of the cluster state under various external fields and interactions, and find that the correction persists unless a phase transition is crossed, or the subsystem symmetry is explicitly broken. Surprisingly, these results uncover that the SSPT order of the cluster state persists beyond the cluster phase, thanks to a new type of subsystem time-reversal symmetry. Finally, we discuss the correction to the area law found in three-dimensional cluster states on different lattices, indicating rich behavior for general subsystem symmetries.