"In this paper, we introduce and numerically simulate a quantum-field-theoretic phenomenon called the gauge ""slingshot"" effect and study its production of gravitational waves. The effect occurs when a source, such as a magnetic monopole or a quark, crosses the boundary between the Coulomb and confining phases. The corresponding gauge field of the source, either electric or magnetic, gets confined into a flux tube stretching in the form of a string (cosmic or a QCD type) that attaches the source to the domain wall separating the two phases. The string tension accelerates the source toward the wall as sort of a slingshot. The slingshot phenomenon is also exhibited by various sources of other codimensionality, such as cosmic strings confined by domain walls or vortices confined by Z2 strings. Apart from the field-theoretic value, the slingshot effect has important cosmological implications, as it provides a distinct source for gravitational waves. The effect is expected to be generic in various extensions of the standard model such as grand unification."

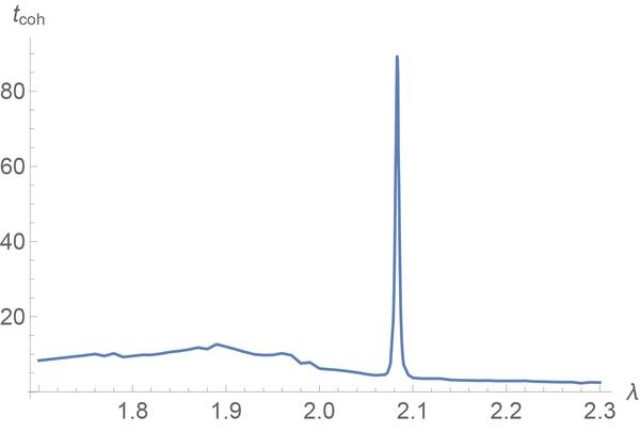
Neutrons and neutrinos are natural probes for new physics. Since they carry no conserved gauge quantum numbers, both can easily mix with the fermions from hidden sectors. A particularly interesting effect is the oscillation of a neutron or a neutrino into a fermion propagating in large extra dimensions. In fact, such a mixing has been identified as the possible origin of small neutrino mass. In this paper, we study neutron oscillations into an extradimensional fermion and show that this effect provides a resonance imaging of the Kaluza-Klein tower. The remarkable feature of this phenomenon is its generic nature: because of a fine spacing of the Kaluza-Klein tower, neutrons at a variety of energy levels, both free or within nuclei, find a bulk oscillation partner. In particular, the partner can be a Kaluza-Klein mode of the same species that gives mass to the neutrino. The existence of bulk states matching the neutron energy levels of nuclear spectra gives rise to tight constraints as well as to potentially observable effects. For a free neutron, we predict recurrent resonant oscillations occurring with the values of the magnetic field correlated with the KK levels. We derive bounds on extra dimensions from ultracold neutron experiments and suggest signatures for refined measurements, which, in particular, can probe the parameter space motivated by the hierarchy problem. Ultracold neutron experiments offer a unique way of Kaluza-Klein spectroscopy.

We study the interactions between 't Hooft-Polyakov magnetic monopoles and the domain walls formed by the same order parameter within an SU(2) gauge theory. We observe that the collision leads to the erasure of the magnetic monopoles, as suggested by Dvali et al. [Phys. Rev. Lett. 80, 2281 (1998)]. The domain wall represents a layer of vacuum with un-Higgsed SU(2) gauge symmetry. When the monopole enters the wall, it unwinds, and the magnetic charge spreads over the wall. We perform numerical simulations of the collision process and, in particular, analyze the angular distribution of the emitted electromagnetic radiation. As in the previous studies, we observe that erasure always occurs. Although not forbidden by any conservation laws, the monopole never passes through the wall. This is explained by entropy suppression. The erasure phenomenon has important implications for cosmology, as it sheds a very different light on the monopole abundance in postinflationary phase transitions and provides potentially observable imprints in the form of electromagnetic and gravitational radiation. The phenomenon also sheds light on fundamental aspects of gauge theories with coexisting phases, such as confining and Higgs phases.

Neutrinoless double beta decay is a textbook example of lepton number violation, often claimed to be a probe of neutrino Majorana mass. However, it could be triggered by new physics,. after all, neutrino Majorana mass requires physics beyond the Standard Model. If at least one electron were right-handed, it would automatically signify new physics rather than neutrino mass. In case both electrons were left-handed, the situation would become rather complicated, and additional effort would be needed to untangle the source for this process. We offer a comprehensive study of this issue from both the effective operator approach and the possible UV completions, including the Pati-Salam quark-lepton unification. While neutrino exchange is natural and physically preferred, our findings show that new physics can still be responsible for the neutrinoless double beta decay. In particular, the Pati-Salam theory can do the job, consistently with all the phenomenological and unification constraints, as long as the unification scale lies above 1012 GeV, albeit at the price of fine-tuning of some scalar masses.

In this work, we study the annihilation of a pair of 't Hooft-Polyakov monopoles due to confinement by a string. We analyze the regime in which the scales of monopoles and strings are comparable. We compute the spectrum of the emitted gravitational waves and find it to agree with the previously calculated pointlike case for wavelengths longer than the system width and before the collision. However, we observe that in a head-on collision, monopoles are never recreated. Correspondingly, not even once the string oscillates. Instead, the system decays into waves of Higgs and gauge fields. We explain this phenomenon by the loss of coherence in the annihilation process. Due to this, the entropy suppression makes the recreation of a monopole pair highly improbable. We argue that in a similar regime, analogous behavior is expected for the heavy quarks connected by a QCD string. There too, instead of restretching a long string after the first collapse, the system hadronizes and decays in a high multiplicity of mesons and glueballs. We discuss the implications of our results.

The interaction of defects can lead to a phenomenon of erasure. During this process, a lower-dimensional object gets absorbed and dissolved by a higher-dimensional one. The phenomenon is very general and has a wide range of implications, both cosmological and fundamental. In particular, all types of strings, such as cosmic strings, QCD flux tubes, or fundamental strings, get erased when encountering a defect, either solitonic or a D-brane that deconfines their fluxes. This leads to a novel mechanism of cosmic string breakup, accompanied by gravitational and electromagnetic radiations. The arguments based on loss of coherence and the entropy count suggest that the erasure probability is very close to one, and strings never make it through the deconfining layer. We confirm this by a numerical simulation of the system, which effectively captures the essence of the phenomenon: a 2 + 1-dimensional problem of interaction between a Nielsen-Olesen vortex of a U(1) Higgs model and a domain wall, inside which the U(1) gauge group is un-Higgsed and the magnetic flux is deconfined. In accordance with the entropy argument, in our simulation, the vortex never makes it across the wall.

We study the formation and evolution of topological defects that arise in the postrecombination phase transition predicted by the gravitational neutrino mass model in Dvali and Funcke [Phys. Rev. D 93 , 113002 (2016)]. In the transition, global skyrmions, monopoles, strings, and domain walls form due to the spontaneous breaking of the neutrino flavor symmetry. These defects are unique in their softness and origin,. as they appear at a very low energy scale, they only require standard model particle content, and they differ fundamentally depending on the Majorana or Dirac nature of the neutrinos. One of the observational signatures is the time dependence and space dependence of the neutrino mass matrix, which could be observable in future neutrino experiments. Already existing data rule out parts of the parameter space in the Majorana case. The detection of this effect could shed light onto the open question of the Dirac versus Majorana neutrino nature.

In some instances of study of quantum evolution of classical backgrounds it is considered inevitable to resort to nonperturbative methods at the price of treating the system semiclassically. We show that a fully quantum perturbative treatment, in which the background is resolved as a multiparticle state, recovers the semiclassical nonperturbative results and allows going beyond. We reproduce particle creation by a classical field in a theory of two scalars as well as in scalar QED in terms of scattering processes of high multiplicity. The multiparticle treatment also gives a transparent picture of why a single-process transition from a classical to a quantum state, which we call quantumization, is exponentially suppressed, whereas the opposite process, classicalization, can take place swiftly if the microstate degeneracy of the classical state is high. An example is provided by the N-graviton portrait of a black hole: a black hole can form efficiently via a 2 -N classicalization process in the collision of high-energy particles, but its quantumization via a decay N -2 is exponentially suppressed.

We argue that black holes admit vortex structure. This is based both on a graviton-condensate description of a black hole as well as on a correspondence between black holes and generic objects with maximal entropy compatible with unitarity, so-called saturons. We show that due to vorticity, a Q-ball-type saturon of a calculable renormalizable theory obeys the same extremality bound on the spin as the black hole. Correspondingly, a black hole with extremal spin emerges as a graviton condensate with vorticity. This offers a topological explanation for the stability of extremal black holes against Hawking evaporation. Next, we show that in the presence of mobile charges, the global vortex traps a magnetic flux of the gauge field. This can have macroscopically observable consequences. For instance, the most powerful jets observed in active galactic nuclei can potentially be accounted for. As a signature, such emissions can occur even without a magnetized accretion disk surrounding the black hole. The flux entrapment can provide an observational window to various hidden sectors, such as millicharged dark matter.

Black holes are considered to be exceptional due to their time evolution and information processing. However, it was proposed recently that these properties are generic for objects, the so-called saturons, that attain the maximal entropy permitted by unitarity. In the present paper, we verify this connection within a renormalizable SU(N) invariant theory. We show that the spectrum of the theory contains a tower of bubbles representing bound states of SU(N) Goldstones. Despite the absence of gravity, a saturated bound state exhibits a striking correspondence with a black hole: Its entropy is given by the Bekenstein-Hawking formula,. semiclassically, the bubble evaporates at a thermal rate with a temperature equal to its inverse radius,. the information retrieval time is equal to Page's time. The correspondence goes through a trans-theoretic entity of the Poincare Goldstone. The black hole-saturon correspondence has important implications for black hole physics, both fundamental and observational.

"We discuss a remarkable correspondence between the description of black holes as highly occupied condensates of N weakly interacting gravitons and that of color glass condensates (CGCs) as highly occupied gluon states. In both cases, the dynamics of ""wee partons"" in Regge asymptotics is controlled by emergent semihard scales that lead to perturbative unitarization and classicalization of 2 -> N particle amplitudes at weak coupling. In particular, they attain a maximal entropy permitted by unitarity, bounded by the inverse coupling alpha of the respective constituents. Strikingly, this entropy is equal to the area measured in units of the Goldstone constant corresponding to the spontaneous breaking of Poincare symmetry by the corresponding graviton or gluon condensate. In gravity, the Goldstone constant is the Planck scale, and gives rise to the Bekenstein-Hawking entropy. Likewise, in the CGC, the corresponding Goldstone scale is determined by the onset of gluon screening. We point to further similarities in black hole formation, thermalization and decay, to that of the glasma matter formed from colliding CGCs in ultrarelativistic nuclear collisions, which decays into a quark-gluon plasma."

It has been argued recently that objects of maximal microstate entropy permitted by unitarity, the so-called saturons, have properties similar to black holes. We demonstrate the existence of such objects in the Gross-Neveu model. From the large-N scaling of S-matrix, we deduce the connection between the entropy of the bound state and the unitarity of scattering. We observe that upon saturation of unitarity, the bound state exhibits a remarkable correspondence with a black hole. The scaling of its entropy is identical to Bekenstein-Hawking entropy. The saturon decays via Hawking's thermal rate of temperature given by the inverse size. The information retrieval time from the Gross-Neveu saturon is isomorphic to Page's time. Our observations indicate that black hole properties are exhibited by saturated states in simple calculable models.

We present certain universal bounds on the capacity of quantum information storage and on the time scale of its retrieval for a generic quantum field theoretic system. The capacity, quantified by the microstate entropy, is bounded from above by the surface area of the object measured in units of a Goldstone decay constant. The Goldstone bosons are universally present due to the spontaneous breaking of Poincare and internal symmetries by the information-storing object. Applied to a black hole, the bound reproduces the Bekenstein-Hawking entropy. However, the relation goes beyond gravity. The minimal time-scale required for retrieving the quantum information from a system is equal to its volume measured in units of the same Goldstone scale. For a black hole, this reproduces the Page time as well as the quantum break-time. Again, the expression for the information retrieval time is very general and is shared by non-gravitational saturated states in gauge theories including QCD. All such objects exhibit universal signatures such as the emission of ultra-soft radiation. Similar bounds apply to non-relativistic many-body systems. This article is part of the theme issue 'Quantum technologies in particle physics'.

Using properties of Goldstino, we show that in generic grand unified theories with gravity-mediated supersymmetry breaking the μ-problem is nonexistent. What happens is that supersymmetry breaking universally induces the shifts of the heavy fields that generate μ and Bμ terms. In the leading order, these are given by the mass of gravitino and are insensitive to the scale of grand unification. The mechanism works regardless whether doublet-triplet splitting is achieved via fine-tuning or not. Moreover, we illustrate this general phenomenon on explicit examples of theories that achieve doublet-triplet splitting dynamically. These include the theories with Higgs doublet as a pseudo-Goldstone boson, as well as the approach based on spontaneous decoupling of the light color triplet from quarks and leptons.

The S -matrix formulation indicates that a consistent embedding of the de Sitter state in quantum gravity is possible exclusively as an excited quantum state constructed on top of a valid S -matrix vacuum such as the Minkowski vacuum. In the present paper we offer such a construction of the de Sitter state in the form of a coherent state of gravitons. Unlike previous realizations of this idea, we focus on BRST invariance as the guiding principle for physicality. In order to establish the universal rules of gauge consistency, we study the BRST-invariant construction of coherent states created by classical and quantum sources in QED and in linearized gravity. Introduction of N copies of scalar matter coupled to gravity allows us to take a special double scaling limit, a so-called species limit, in which our construction of the de Sitter state becomes exact. In this limit, the irrelevant quantum gravitational effects vanish, whereas the collective phenomena, such as Gibbons-Hawking radiation, are calculable.

A mechanism for the formation of primordial black holes is proposed. Here, heavy quarks of a confining gauge theory produced by de Sitter fluctuations are pushed apart by inflation and get confined after horizon reentry. The large amount of energy stored in the color flux tubes connecting the quark pair leads to black-hole formation. These are much lighter and can be of higher spin than those produced by standard collapse of horizon-size inflationary overdensities. Other difficulties exhibited by such mechanisms are also avoided. Phenomenological features of the new mechanism are discussed as well as accounting for both the entirety of the dark matter and the supermassive black holes in the galactic centers. Under proper conditions, the mechanism can be realized in a generic confinement theory, including ordinary QCD. We discuss a possible string-theoretic realization via D-branes. Interestingly, for conservative values of the string scale, the produced gravity waves are within the range of recent NANOGrav data. Simple generalizations of the mechanism allow for the existence of a significant scalar component of gravity waves with distinct observational signatures.

The cosmological constant puzzle, traditionally viewed as a naturalness problem, is evidently nullified by the S-matrix formulation of quantum gravity/string theory. We point out an implication of this fact for another naturalness puzzle, the Hierarchy Problem between the weak and Planck scales. By eliminating the landscape of de Sitter vacua and eternal inflation, the S-matrix formulation exhibits an obvious tension with the explanations based on anthropic selection or cosmological relaxation of the Higgs mass. This sharpens the Hierarchy Problem in a profound way. On one hand, it strengthens the case for explanations based on new physics not far from the weak scale. At the same time, it opens up a question, whether instead the hierarchy is imposed by the S-matrix consistency between the Standard Model and gravity.

A large number of particle species allows to formulate quantum gravity in a special double-scaling limit, the species limit. In this regime, quantum gravitational amplitudes simplify substantially. An infinite set of perturbative corrections, that usually blur the picture, vanishes, whereas the collective and non-perturbative effects can be cleanly extracted. Such are the effects that control physics of black holes and of de Sitter and their entanglement curves. In string theory example, we show that the entropy of open strings matches the Gibbons-Hawking entropy of a would-be de Sitter state at the point of saturation of the species bound. This shows, from yet another angle, why quantum gravity/string theory cannot tolerate a de Sitter vacuum. Finally, we discuss various observational implications.

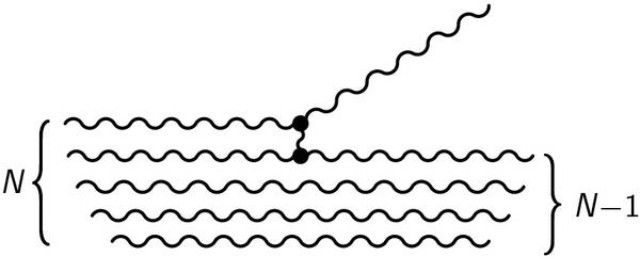
We establish that unitarity of scattering amplitudes imposes universal entropy bounds. The maximal entropy of a self-sustained quantum field object of radius R is equal to its surface area and at the same time to the inverse running coupling alpha evaluated at the scale R. The saturation of these entropy bounds is in one-to-one correspondence with the non-perturbative saturation of unitarity by 2 -> N particle scattering amplitudes at the point of optimal truncation. These bounds are more stringent than Bekenstein's bound and in a consistent theory all three get saturated simultaneously. This is true for all known entropy-saturating objects such as solitons, instantons, baryons, oscillons, black holes or simply lumps of classical fields. We refer to these collectively as saturons and show that in renormalizable theories they behave in all other respects like black holes. Finally, it is argued that the confinement in SU(N) gauge theory can be understood as a direct consequence of the entropy bounds and unitarity.

S-matrix formulation of gravity excludes de Sitter vacua. In particular, this is organic to string theory. The S-matrix constraint is enforced by an anomalous quantum break-time proportional to the inverse values of gravitational and/or string couplings. Due to this, de Sitter can satisfy the conditions for a valid vacuum only at the expense of trivializing the graviton and closed-string S-matrices. At non-zero gravitational and string couplings, de Sitter is deformed by corpuscular 1/N effects, similarly to Witten-Veneziano mechanism in QCD with N colors. In this picture, an S-matrix formulation of Einstein gravity, such as string theory, nullifies an outstanding cosmological puzzle. We discuss possible observational signatures which are especially interesting in theories with a large number of particle species. Species can enhance the primordial quantum imprints to potentially observable level even if the standard inflaton fluctuations are negligible.

We show that non-perturbative entities such as solitons and instantons saturate bounds on entropy when the theory saturates unitarity. Simultaneously, the entropy becomes equal to the area of the soliton/instanton. This is strikingly similar to black hole entropy despite absence of gravity. We explain why this similarity is not an accident. We present a formulation that allows to apply the entropy bound to instantons. The new formulation also eliminates apparent violations of the Bekenstein entropy bound by some otherwise-consistent unitary systems. We observe that in QCD, an isolated instanton of fixed size and position violates the entropy bound for strong 't Hooft coupling. At critical 't Hooft coupling the instanton entropy is equal to its area.

"Quantum field theories with exact but spontaneously broken conformal invariance have an intriguing feature: their vacuum energy (cosmological constant) is equal to zero. Up to now, the only known ultraviolet complete theories where conformal symmetry can be spontaneously broken were associated with supersymmetry (SUSY), with the most prominent example being the N=4 SUSY Yang-Mills. In this Letter we show that the recently proposed conformal ""fishnet"" theory supports at the classical level a rich set of flat directions (moduli) along which conformal symmetry is spontaneously broken. We demonstrate that, at least perturbatively, some of these vacua survive in the full quantum theory (in the planar limit, at the leading order of 1/N-c expansion) without any fine tuning. The vacuum energy is equal to zero along these flat directions, providing the first non-SUSY example of a four-dimensional quantum field theory with ""natural"" breaking of conformal symmetry. (C) 2020 The Authors. Published by Elsevier B.V."

Systems of enhanced memory capacity are subjected to a universal effect of memory burden, which suppresses their decay. In this paper, we study a prototype model to show that memory burden can be overcome by rewriting stored quantum information from one set of degrees of freedom to another one. However, due to a suppressed rate of rewriting, the evolution becomes extremely slow compared to the initial stage. Applied to black holes, this predicts a metamorphosis, including a drastic deviation from Hawking evaporation, at the latest after losing half of the mass. This raises a tantalizing question about the fate of a black hole. As two likely options, it can either become extremely long lived or decay via a new classical instability into gravitational lumps. The first option would open up a new window for small primordial black holes as viable dark matter candidates.

Decoupling of heavy modes in effective low energy theory is one of the most fundamental concepts in physics. It tells us that modes must have a negligible effect on the physics of gravitational backgrounds with curvature radius larger than their wavelengths. Despite this, there exist claims that trans-Planckian modes put severe bound on the duration of inflation even when the Hubble parameter is negligible as compared to the Planck mass. If true, this would mean that inflation violates the principle of decoupling or at least requires its reformulation. We clarify the fundamental misconception on which these bounds are based and respectively refute them. Our conclusion is that inflation fully falls within the validity of a reliable effective field theory treatment and does not suffer from any spurious trans-Planckian problem.

We propose a novel class of compact dark matter objects in theories where the dark matter consists of multiple sectors. We call these objects N-MACHOs. In such theories neither the existence of dark matter species nor their extremely weak coupling to the observable sector represent additional hypotheses but instead are imposed by the solution to the Hierarchy Problem and unitarity. The crucial point is that particles from the same sector have nontrivial interactions but interact only gravitationally otherwise. As a consequence, the pressure that counteracts the gravitational collapse is reduced while the gravitational force remains the same. This results in collapsed structures much lighter and smaller as compared to the ordinary single-sector case. We apply this phenomenon to a dark matter theory that consists of N dilute copies of the Standard Model. The solutions do not rely on an exotic stabilization mechanism, but rather use the same well-understood properties as known stellar structures. This framework also gives rise to new microscopic superheavy structures, for example with mass 10(8) g and size 10(-13) cm. By confronting the resulting objects with observational constraints, we find that, due to a huge suppression factor entering the mass spectrum, these objects evade the strongest constrained region of the parameter space. Finally, we discuss possible formation scenarios of N-MACHOs. We argue that, due to the efficient dissipation of energy on small scales, high-density regions such as ultracompact minihalos could serve as formation sites of N-MACHOs.

In post LHC era the old idea of cosmological vacuum relaxation of the Higgs mass that does not require any new physics in the vicinity of LHC energies acquires a new meaning. I discuss how this concept of naturanless differs from the standard one by 't Hooft. Here the observed value of the Higgs mass corresponds to a vacuum of infinite degeneracy and infinite entropy. Therefore, it represents and attractor point of cosmic inflationary evolution. This information is unavailable for a low energy observer living in one of such vacua. By not seeing any stabilizing physics at LHC such an observer is puzzled and creates an artificial problem of naturalness which in reality does not exist. We explain why this solution is fully compatible with the concept of Wilsonian decoupling.

Elementary particles of large spin s store quantum information in degenerate states and therefore are subject to the Bekenstein entropy bound. We observe that for sufficiently large s the bound is violated unless the particle acquires a new associated length-scale different from its Compton wavelength. This can be regarded as a glimpse of stringiness. Moreover, this bound is independent of gravity. The inclusion of gravity additionally generates a new scale at which the thermality of the black hole radiation is violated by the emission of a high spin particle. This bound can be understood as the black hole species bound, i.e. an induced quantum gravity cutoff-scale given by MP/s√. The two bounds carry qualitatively different information.