Quantum Information Orbitals (QIO): Unveiling Intrinsic Many-Body Complexity by Compressing Single-Body Triviality
K. Liao, L. X. Ding, C. Schilling
Journal of Physical Chemistry Letters 15 (26), 6782-6790 (2024).
The simultaneous treatment of static and dynamic correlations in strongly correlated electron systems is a critical challenge. In particular, finding a universal scheme for identifying a single-particle orbital basis that minimizes the representational complexity of the many-body wave function is a formidable and longstanding problem. As a contribution toward its solution, we show that the total orbital correlation actually reveals and quantifies the intrinsic complexity of the wave function, once it is minimized via orbital rotations. To demonstrate the power of this concept in practice, an iterative scheme is proposed to optimize the orbitals by minimizing the total orbital correlation calculated by the tailored coupled cluster singles and doubles (TCCSD) ansatz. The optimized orbitals enable the limited TCCSD ansatz to capture more nontrivial information on the many-body wave function, indicated by the improved wave function and energy. An initial application of this scheme shows great improvement of TCCSD in predicting the singlet ground state potential energy curves of the strongly correlated C-2 and Cr-2 molecule.

Physical entanglement between localized orbitals
L. X. Ding, G. Duennweber, C. Schilling
Quantum Science and Technology 9 (1), 15005 (2024).
The goal of the present work is to guide the development of quantum technologies in the context of fermionic systems. For this, we first elucidate the process of entanglement swapping in electron systems such as atoms, molecules or solid bodies. This demonstrates the significance of the number-parity superselection rule and highlights the relevance of localized few-orbital subsystems for quantum information processing tasks. Then, we explore and quantify the entanglement between localized orbitals in two systems, a tight-binding model of non-interacting electrons and the hydrogen ring. For this, we apply the first closed formula of a faithful entanglement measure, derived in (arXiv:2207.03377) as an extension of the von Neumann entropy to genuinely correlated many-orbital systems. For both systems, long-distance entanglement is found at low and high densities eta, whereas for medium densities, eta approximate to 12 , practically only neighboring orbitals are entangled. The Coulomb interaction does not change the entanglement pattern qualitatively except for low and high densities where the entanglement increases as function of the distance between both orbitals.

Quantum Information-Assisted Complete Active Space Optimization (QICAS)
L. X. Ding, S. Knecht, C. Schilling
Journal of Physical Chemistry Letters 14 (49), 11022-11029 (2023).
We propose an effective quantum information-assisted complete active space optimization scheme (QICAS). What sets QICAS apart from other correlation-based selection schemes is (i) the use of unique measures from quantum information that assess the correlation in electronic structures in an unambiguous and predictive manner and (ii) an orbital optimization step that minimizes the correlation discarded by the active space approximation. Equipped with these features, QICAS yields, for smaller correlated molecule, sets of optimized orbitals with respect to which the complete active space configuration interaction energy reaches the corresponding complete active space self-consistent field (CASSCF) energy within chemical accuracy. For more challenging systems such as the chromium dimer, QICAS offers an excellent starting point for CASSCF by greatly reducing the number of iterations required for numerical convergence. Accordingly, our study validates a profound empirical conjecture: the energetically optimal nonactive spaces are predominantly those that contain the least entanglement.

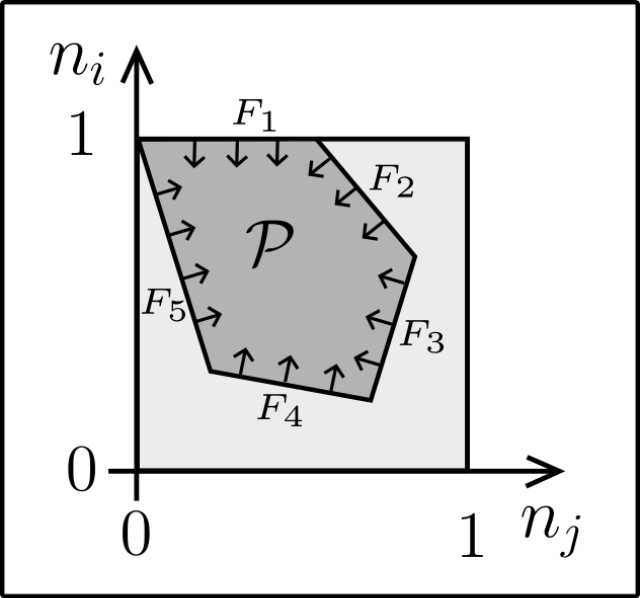
An Effective Solution to Convex 1-Body N-Representability
F. Castillo, J. P. Labbé, J. Liebert, A. Padrol, E. Philippe, C. Schilling
Annales Henri Poincare 24 (7), 2241-2321 (2023).
From a geometric point of view, Pauli's exclusion principle de -fines a hypersimplex. This convex polytope describes the compatibility of 1-fermion and N-fermion density matrices,. therefore, it coincides with the convex hull of the pure N-representable 1-fermion density matrices. Consequently, the description of ground state physics through 1-fermion density matrices may not necessitate the intricate pure state generalized Pauli constraints. In this article, we study the generalization of the 1-body N-representability problem to ensemble states with fixed spectrum w, in order to describe finite-temperature states and distinctive mixtures of ex-cited states. By employing ideas from convex analysis and combinatorics, we present a comprehensive solution to the corresponding convex relaxation, thus circumventing the complexity of generalized Pauli constraints. In particular, we adapt and further develop tools such as symmetric poly-topes, sweep polytopes, and Gale order. For both fermions and bosons, generalized exclusion principles are discovered, which we determine for any number of particles and dimension of the 1-particle Hilbert space. These exclusion principles are expressed as linear inequalities satisfying hierarchies determined by the nonzero entries of w. The two families of polytopes resulting from these inequalities are part of the new class of so-called lineup polytopes.

Refining and relating fundamentals of functional theory
J. Liebert, A. Y. Chaou, C. Schilling
Journal of Chemical Physics 158 (21), 214108 (2023).
To advance the foundation of one-particle reduced density matrix functional theory (1RDMFT), we refine and relate some of its fundamental features and underlying concepts. We define by concise means the scope of a 1RDMFT, identify its possible natural variables, and explain how symmetries could be exploited. In particular, for systems with time-reversal symmetry, we explain why there exist six equivalent universal functionals, prove concise relations among them, and conclude that the important notion of v-representability is relative to the scope and choice of variable. All these fundamental concepts are then comprehensively discussed and illustrated for the Hubbard dimer and its generalization to arbitrary pair interactions W. For this, we derive by analytical means the pure and ensemble functionals with respect to both the real- and complex-valued Hilbert space. The comparison of various functionals allows us to solve the underlying v-representability problems analytically, and the dependence of its solution on the pair interaction is demonstrated. Intriguingly, the gradient of each universal functional is found to always diverge repulsively on the boundary of the domain. In that sense, this key finding emphasizes the universal character of the fermionic exchange force, recently discovered and proven in the context of translationally invariant one-band lattice models.

Deriving density-matrix functionals for excited states
J. Liebert, C. Schilling
Scipost Physics 14 (5), 120 (2023).
We initiate the recently proposed w-ensemble one-particle reduced density matrix func-tional theory (w-RDMFT) by deriving the first functional approximations and illustrate how excitation energies can be calculated in practice. For this endeavour, we first study the symmetric Hubbard dimer, constituting the building block of the Hubbard model, for which we execute the Levy-Lieb constrained search. Second, due to the particular suit-ability of w-RDMFT for describing Bose-Einstein condensates, we demonstrate three con-ceptually different approaches for deriving the universal functional in a homogeneous Bose gas for arbitrary pair interaction in the Bogoliubov regime. Remarkably, in both systems the gradient of the functional is found to diverge repulsively at the boundary of the functional's domain, extending the recently discovered Bose-Einstein condensation force to excited states. Our findings highlight the physical relevance of the generalized exclusion principle for fermionic and bosonic mixed states and the curse of universality in functional theories.

An Effective Solution to Convex 1-Body N-Representability
F. Castillo, J. P. Labbe, J. Liebert, A. Padrol, E. Philippe, C. Schilling
Annales Henri Poincare 81 (2023).
From a geometric point of view, Pauli's exclusion principle de -fines a hypersimplex. This convex polytope describes the compatibility of 1-fermion and N-fermion density matrices,. therefore, it coincides with the convex hull of the pure N-representable 1-fermion density matrices. Consequently, the description of ground state physics through 1-fermion density matrices may not necessitate the intricate pure state generalized Pauli constraints. In this article, we study the generalization of the 1-body N-representability problem to ensemble states with fixed spectrum w, in order to describe finite-temperature states and distinctive mixtures of ex-cited states. By employing ideas from convex analysis and combinatorics, we present a comprehensive solution to the corresponding convex relaxation, thus circumventing the complexity of generalized Pauli constraints. In particular, we adapt and further develop tools such as symmetric poly-topes, sweep polytopes, and Gale order. For both fermions and bosons, generalized exclusion principles are discovered, which we determine for any number of particles and dimension of the 1-particle Hilbert space. These exclusion principles are expressed as linear inequalities satisfying hierarchies determined by the nonzero entries of w. The two families of polytopes resulting from these inequalities are part of the new class of so-called lineup polytopes.

1-Matrix functional for long-range interaction energy of two hydrogen atoms
J. Cioslowski, C. Schilling, R. Schilling
Journal of Chemical Physics 158 (8), 84106 (2023).
"The leading terms in the large-R asymptotics of the functional of the one-electron reduced density matrix for the ground-state energy of the H-2 molecule with the internuclear separation R are derived thanks to the solution of the phase dilemma at the R -> infinity limit. At this limit, the respective natural orbitals (NOs) are given by symmetric and antisymmetric combinations of ""half-space "" orbitals with the corresponding natural amplitudes having the same amplitudes but opposite signs. Minimization of the resulting explicit functional yields the large-R asymptotics for the occupation numbers of the weakly occupied NOs and the C-6 dispersion coefficient. The highly accurate approximates for the radial components of the p-type ""half-space "" orbitals and the corresponding occupation numbers (that decay like R-6), which are available for the first time thanks to the development of the present formalism, have some unexpected properties."

An exact one-particle theory of bosonic excitations: from a generalized Hohenberg-Kohn theorem to convexified N-representability
J. Liebert, C. Schilling
New Journal of Physics 25 (1), 13009 (2023).
Motivated by the Penrose-Onsager criterion for Bose-Einstein condensation we propose a functional theory for targeting low-lying excitation energies of bosonic quantum systems through the one-particle picture. For this, we employ an extension of the Rayleigh-Ritz variational principle to ensemble states with spectrum w and prove a corresponding generalization of the Hohenberg-Kohn theorem: the underlying one-particle reduced density matrix determines all properties of systems of N identical particles in their w -ensemble states. Then, to circumvent the v-representability problem common to functional theories, and to deal with energetic degeneracies, we resort to the Levy-Lieb constrained search formalism in combination with an exact convex relaxation. The corresponding bosonic one-body w -ensemble N-representability problem is solved comprehensively. Remarkably, this reveals a complete hierarchy of bosonic exclusion principle constraints in conceptual analogy to Pauli's exclusion principle for fermions and recently discovered generalizations thereof.

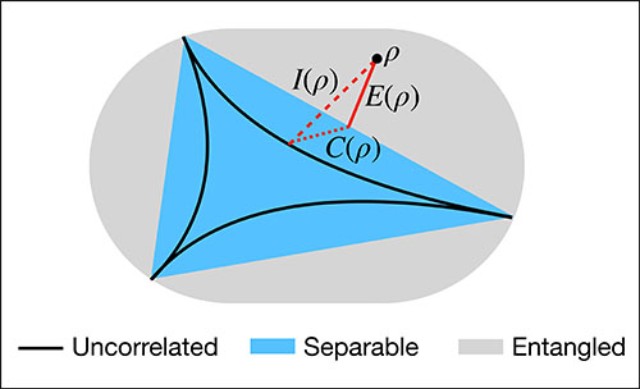
Quantum correlations in molecules: from quantum resourcing to chemical bonding
L. X. Ding, S. Knecht, Z. Zimboras, C. Schilling
Quantum Science and Technology 8 (1), 15015 (2023).
The second quantum revolution is all about exploiting the quantum nature of atoms and molecules to execute quantum information processing tasks. To boost this growing endeavor and by anticipating the key role of quantum chemistry therein, our work establishes a framework for systematically exploring, quantifying and dissecting correlation effects in molecules. By utilizing the geometric picture of quantum states we compare-on a unified basis and in an operationally meaningful way-total, quantum and classical correlation and entanglement in molecular ground states. To unlock and maximize the quantum informational resourcefulness of molecules an orbital optimization scheme is developed, leading to a paradigm-shifting insight: a single covalent bond equates to the entanglement 2ln(2)

Excitations of Quantum Many-Body Systems via Purified Ensembles: A Unitary-Coupled-Cluster-Based Approach
C. L. Benavides-Riveros, L. P. Chen, C. Schilling, S. Mantilla, S. Pittalis
Physical Review Letters 129 (6), 66401 (2022).
State-average calculations based on a mixture of states are increasingly being exploited across chemistry and physics as versatile procedures for addressing excitations of quantum many-body systems. If not too many states should need to be addressed, calculations performed on individual states are also a common option. Here we show how the two approaches can be merged into one method, dealing with a generalized yet single pure state. Implications in electronic structure calculations are discussed and for quantum computations are pointed out.

Foundation of One-Particle Reduced Density Matrix Functional Theory for Excited States
J. Liebert, F. Castillo, J. P. Labbe, C. Schilling
Journal of Chemical Theory and Computation 18 (1), 124-140 (2022).
In Phys. Rev. Lett. 2021, 127, 023001 a reduced density matrix functional theory (RDMFT) was proposed for calculating energies of selected eigenstates of interacting many-Fermion systems. Here, we develop a solid foundation for this so-called w-RDMFT and present the details of various derivations. First, we explain how a generalization of the Ritz variational principle to ensemble states with fixed weights w in combination with the constrained search would lead to a universal functional of the one-particle reduced density matrix. To turn this into a viable functional theory, however, we also need to implement an exact convex relaxation. This general procedure includes Valone's pioneering work on ground state RDMFT as the special case w = (1,0, ...). Then, we work out in a comprehensive manner a methodology for deriving a compact description of the functional's domain. This leads to a hierarchy of generalized exclusion principle constraints which we illustrate in great detail. By anticipating their future pivotal role in functional theories and to keep our work self-contained, several required concepts from convex analysis are introduced and discussed.

Fermionic systems for quantum information people
S. Szalay, Z. Zimboras, M. Mate, G. Barcza, C. Schilling, O. Legeza
Journal of Physics a-Mathematical and Theoretical 54 (39), 393001 (2021).
The operator algebra of fermionic modes is isomorphic to that of qubits, the difference between them is twofold: the embedding of subalgebras corresponding to mode subsets and multiqubit subsystems on the one hand, and the parity superselection in the fermionic case on the other. We discuss these two fundamental differences extensively, and illustrate these through the Jordan-Wigner representation in a coherent, self-contained, pedagogical way, from the point of view of quantum information theory. Our perspective leads us to develop useful new tools for the treatment of fermionic systems, such as the fermionic (quasi-)tensor product, fermionic canonical embedding, fermionic partial trace, fermionic products of maps and fermionic embeddings of maps. We formulate these by direct, easily applicable formulas, without mode permutations, for arbitrary partitionings of the modes. It is also shown that fermionic reduced states can be calculated by the fermionic partial trace, containing the proper phase factors. We also consider variants of the notions of fermionic mode correlation and entanglement, which can be endowed with the usual, local operation based motivation, if the parity superselection rule is imposed. We also elucidate some other fundamental points, related to joint map extensions, which make the parity superselection inevitable in the description of fermionic systems.

Ensemble Reduced Density Matrix Functional Theory for Excited States and Hierarchical Generalization of Pauli's Exclusion Principle
C. Schilling, S. Pittalis
Physical Review Letters 127 (2), 23001 (2021).
We propose and work out a reduced density matrix functional theory (RDMFT) for calculating energies of eigenstates of interacting many-electron systems beyond the ground state. Various obstacles which historically have doomed such an approach to be unfeasible are overcome. First, we resort to a generalization of the Ritz variational principle to ensemble states with fixed weights. This in combination with the constrained search formalism allows us to establish a universal functional of the one-particle reduced density matrix. Second, we employ tools from convex analysis to circumvent the too involved N-representability constraints. Remarkably, this identifies Valone's pioneering work on RDMFT as a special case of convex relaxation and reveals that crucial information about the excitation structure is contained in the functional's domain. Third, to determine the crucial latter object, a methodology is developed which eventually leads to a generalized exclusion principle. The corresponding linear constraints are calculated for systems of arbitrary size.

Functional theory for Bose-Einstein condensates
J. Liebert, C. Schilling
Physical Review Research 3 (1), 13282 (2021).
One-particle reduced density matrix functional theory would potentially be the ideal approach for describing Bose-Einstein condensates. It namely replaces the macroscopically complex wave function by the simple one-particle reduced density matrix, and therefore provides direct access to the degree of condensation and still recovers quantum correlations in an exact manner. We initiate and establish this theory by deriving the respective universal functional F for homogeneous Bose-Einstein condensates with arbitrary pair interaction. Most importantly, the successful derivation necessitates a particle-number conserving modification of Bogoliubov theory and a solution of the common phase dilemma of functional theories. We then illustrate this approach in several bosonic systems such as homogeneous Bose gases and the Bose-Hubbard model. Remarkably, the general form of F reveals the existence of a universal Bose-Einstein condensation force which provides an alternative and more fundamental explanation for quantum depletion.

How creating one additional well can generate Bose-Einstein condensation
M. Máté, Ö. Legeza, R. Schilling, M. Yousif, C. Schilling
Communications Physics 4, 29 (2021).
The realization of Bose-Einstein condensation in ultracold trapped gases has led to a revival of interest in this fascinating quantum phenomenon. This experimental achievement necessitated both extremely low temperatures and sufficiently weak interactions. Particularly in reduced spatial dimensionality even an infinitesimal interaction immediately leads to a departure to quasi-condensation. We propose a system of strongly interacting bosons, which overcomes those obstacles by exhibiting a number of intriguing related features: (i) The tuning of just a single control parameter drives a transition from quasi-condensation to complete condensation, (ii) the destructive influence of strong interactions is compensated by the respective increased mobility, (iii) topology plays a crucial role since a crossover from one- to ‘infinite’-dimensionality is simulated, (iv) a ground state gap opens, which makes the condensation robust to thermal noise. Remarkably, all these features can be derived by analytical and exact numerical means despite the non-perturbative character of the system.

Concept of Orbital Entanglement and Correlation in Quantum Chemistry
L. X. Ding, S. Mardazad, S. Das, S. Szalay, U. Schollwöck, Z. Zimboras, C. Schilling
Journal of Chemical Theory and Computation 17 (1), 79-95 (2021).
A recent development in quantum chemistry has established the quantum mutual information between orbitals as a major descriptor of electronic structure. This has already facilitated remarkable improvements in numerical methods and may lead to a more comprehensive foundation for chemical bonding theory. Building on this promising development, our work provides a refined discussion of quantum information theoretical concepts by introducing the physical correlation and its separation into classical and quantum parts as distinctive quantifiers of electronic structure. In particular, we succeed in quantifying the entanglement. Intriguingly, our results for different molecules reveal that the total correlation between orbitals is mainly classical, raising questions about the general significance of entanglement in chemical bonding. Our work also shows that implementing the fundamental particle number superselection rule, so far not accounted for in quantum chemistry, removes a major part of correlation and entanglement seen previously. In that respect, realizing quantum information processing tasks with molecular systems might be more challenging than anticipated.