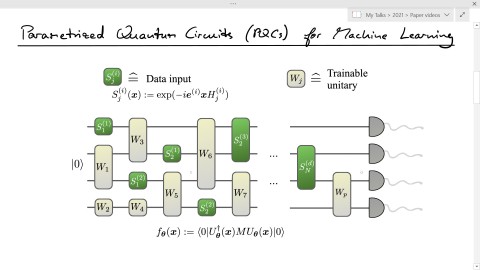
Encoding-dependent generalization bounds for parametrized quantum circuits

A large body of recent work has begun to explore the potential of parametrized quantum circuits (PQCs) as machine learning models, within the framework of hybrid quantum-classical optimization. In particular, theoretical guarantees on the out-of-sample performance of such models, in terms of generalization bounds, have emerged. However, none of these generalization bounds depend explicitly on how the classical input data is encoded into the PQC. We derive generalization bounds for PQC-based models that depend explicitly on the strategy used for data-encoding. These imply bounds on the performance of trained PQC-based models on unseen data. Moreover, our results facilitate the selection of optimal data-encoding strategies via structural risk minimization, a mathematically rigorous framework for model selection. We obtain our generalization bounds by bounding the complexity of PQC-based models as measured by the Rademacher complexity and the metric entropy, two complexity measures from statistical learning theory. To achieve this, we rely on a representation of PQC-based models via trigonometric functions. Our generalization bounds emphasize the importance of well-considered data-encoding strategies for PQC-based models.

Authors: Matthias C. Caro (1,2), Elies Gil-Fuster (3), Johannes Jakob Meyer (3,4), Jens Eisert (3,5), and Ryan Sweke (3)

Affiliations: 1. TU Munich 2. MCQST 3. FU Berlin 4. University of Copenhagen 5. Helmholtz Zentrum Berlin

Error mitigation and quantum-assisted simulation in the error corrected regime

A standard approach to quantum computing is based on the idea of promoting a classically simulable and fault-tolerant set of operations to a universal set by the addition of ‘magic’ quantum states. In this context, we develop a general framework to discuss the value of the available, non-ideal magic resources, relative to those ideally required. We single out a quantity, the Quantum-assisted Robustness of Magic (QRoM), which measures the overhead of simulating the ideal resource with the non-ideal ones through quasiprobability-based methods. This extends er- ror mitigation techniques, originally developed for Noisy Intermediate Scale Quantum (NISQ) devices, to the case where qubits are logically encoded. The QRoM shows how the addition of noisy magic resources allows to boost classical quasiprobability simulations of a quantum circuit and allows the construction of explicit protocols, interpolating between classical simulation and an ideal quantum computer.

Authors: Alessandro Ciani (1,2), Matteo Lostaglio

Affiliations: 1) FZ Juelich 2) TU Delft 3) University of Amsterdam

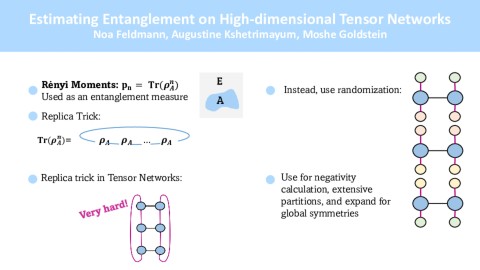
Estimating Entanglement on High Dimensional Tensor Networks

Entanglement is a key property in many-body systems, useful both as a sensitive probe of their physical behavior, and as a measure for their "quantumness", characterizing their usefulness in quantum technologies. Tensor networks are often employed for describing the states of such systems. However, current approaches for the calculation of entanglement measures of tensor network states in two and higher dimensions are highly impractical even for moderate-size systems. In our work, we develop a new method for studying the entanglement of tensor network states in general dimension without fully reconstructing the density matrix. The method requires sampling matrix elements of the reduced density matrix between random states chosen from a finite set. Such matrix elements are straightforward to calculate for tensor network states, and their moments give the Renyi entropies and negativities. We test our method on Kitaev’s exactly solvable toric code model and the one-dimensional XX model, and demonstrate that accurate results can be obtained on a personal computer for relatively large subsystem sizes, and general system partitions. We discuss models for which the method is suited most, such as extensive partitions.

Authors: Noa Feldman[1], Augustine Kshetrimayum[2], Moshe Goldstein[1]

Affiliations: [1] Raymond and Beverly Sackler School of Physics and Astronomy, Tel-Aviv University [2] Dahlem Center for Complex Quantum Systems, Freie Universitat Berlin

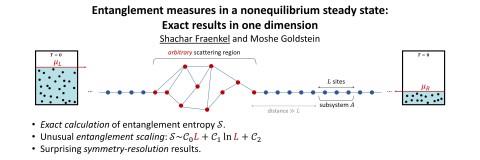
Entanglement Measures in a Nonequilibrium Steady State: Exact Results in One Dimension Childcare

Entanglement plays a prominent role in the study of condensed matter many-body systems: Entanglement measures not only quantify the possible use of these systems in quantum information protocols, but also shed light on their physics. However, exact analytical results remain scarce, especially for systems out of equilibrium. In this work [1] we examine a paradigmatic one-dimensional fermionic system that consists of a uniform tight-binding chain with an arbitrary scattering region near its center, which is subject to a DC bias voltage at zero temperature. The system is thus held in a current-carrying nonequilibrium steady state, which can nevertheless be described by a pure quantum state. Using a generalization of the Fisher-Hartwig conjecture, we present an exact calculation of the bipartite entanglement entropy of a subsystem with its complement, and show that the scaling of entanglement with the length of the subsystem is highly unusual, containing both a volume-law linear term and a logarithmic term. The linear term is related to imperfect transmission due to scattering, while the logarithmic term arises from the Fermi discontinuities in the distribution function. The analytical results are further generalized to accommodate the case of multiple scattering regions. Our analysis also produces an exact expression for the particle-number-resolved entanglement [2]. We find that although to leading order entanglement equipartition applies, the first term breaking it grows with the size of the subsystem, a novel behavior not observed in previously studied systems. The analytical expressions are shown to be in good agreement with numerical calculations. These results pave the way towards the future study of more complicated systems, especially the effects of disorder and localization. [1] S. Fraenkel and M. Goldstein, arXiv:2105.00740 (2021). [2] M. Goldstein and E. Sela, Phys. Rev. Lett. 120, 200602 (2018).

Authors: Shachar Fraenkel and Moshe Goldstein

Affiliations: School of Physics and Astronomy, Tel-Aviv University

Complete Modified Log-Sobolev inequalities

We prove that every GNS-symmetric quantum Markov semigroup on a finite dimensional matrix algebra satisfies a modified log-Sobolev inequality that is stable under tensorization.

Authors: Li Gao and Cambyse Rouze

Affiliations: Technische Universität München

Random access codes via quantum contextual redundancy

We propose a protocol to encode bits in the measurement statistics of parity observables with overlapping contexts. The intrinsic information redundancy of quantum contexts allows for a compressed encoding and efficient retrieval when large entangled states (>18 qubits) perform the encoding. Applications of this protocol include algorithms involving storage of large amounts of data but requiring only partial retrieval of the information, as is the case of decision trees. In particular, we showcase quantum advantage over state-of-the-art information storage capacity for more than 44 qubits, and prove that systems above 100 qubits would suffice to encode a brute force solution for games of chess-like complexity.

Authors: Giancarlo Gatti (1,2), Daniel Huerga (1), Enrique Solano (1,3,4,5), Mikel Sanz (1,4,5)

Affiliations: (1) Department of Physical Chemistry, University of the Basque Country UPV/EHU, Apartado 644, 48080 Bilbao, Spain (2) Quantum Mads, Uribitarte Kalea 6, 48001 Bilbao, Spain (3) International Center of Quantum Artificial Intelligence for Science and Technology (QuArtist) and Department of Physics, Shanghai University, 200444 Shanghai, China (4) IKERBASQUE, Basque Foundation for Science, Plaza Euskadi 5, 48009 Bilbao, Spain (5) IQM, Nymphenburgerstr. 86, 80636 Munich, Germany

Local Transformations of Multiple Multipartite States

Multipartite entanglement can be quantified by considering Local Operations assisted by Classical Communication (LOCC). However, for systems with fixed local dimensions, the partial order induced by LOCC is generically trivial. Consequently, we study a physically motivated extension of LOCC: multi-state LOCC. Here, one considers simultaneous LOCC transformations of finitely many pure states. In the multipartite case, we show one can change the stochastic LOCC (SLOCC) class of the individual states; that one can perform transformations not possible in the single-copy case, transferring entanglement from one state to the other; provide examples of multipartite entanglement catalysis; and find improved probabilistic protocols. In the bipartite case, we numerous find non-trivial LU transformations.

Authors: David Gunn [1], Antoine Neven [1], Martin Hebenstreit [1], Barbara Kraus [1]

Affiliations: [1] University of Innsbruck

State transformations within entanglement classes containing permutation-symmetric states

The study of state transformations under local operations and classical communication (LOCC) plays a crucial role in entanglement theory. While this has been long ago characterized for pure bipartite states, the situation is drastically different for systems of more parties: generic pure qudit states cannot be obtained from nor transformed to any state, which contains a different amount of entanglement. We consider here the question of LOCC convertibility for permutation-symmetric pure states of an arbitrary number of parties and local dimension, a class of clear interest both from physical and mathematical reasons and for which the aforementioned result does not apply given that it is a zero-measure subset in the state space. While it turns out that this situation persists for generic n-qubit symmetric states, we consider particular families for which we can determine that on the contrary they are endorsed with a rich local stabilizer, a necessary requirement for LOCC convertibility to be possible. This allows us to identify classes in which LOCC transformations among permutation-symmetric states are possible. Notwithstanding, we provide several results that indicate severe obstructions to LOCC convertibility in general even within these highly symmetrical classes. The only classes found for which every state can be converted to a more weakly entangled state are the n-qubit GHZ and W classes. In the course of the study of LOCC transformations we also characterize the local symmetries of symmetric states.

Authors: Martin Hebenstreit(1), Cornelia Spee(1), Nicky Kai Hong Li(1), Julio I. de Vicente(2), Barbara Kraus(1)

Affiliations: (1) Institute for Theoretical Physics, University of Innsbruck, Technikerstr. 21A, 6020 Innsbruck, Austria (2) Departamento de Matemáticas, Universidad Carlos III de Madrid, Avda. de la Universidad 30, E-28911, Leganés (Madrid), Spain

Bosonic Dirty Paper Coding

The bosonic channel is addressed with modulation interference and side information at the transmitter. The model can be viewed as the quantum counterpart of the classical random-parameter Gaussian channel. Based on Costa’s writing-on-dirty-paper result (1983), the effect of the interference can be canceled. For both homodyne and heterodyne detection, we observe the same phenomenon, as the model reduces to a classical Gaussian channel. Then, we consider the bosonic channel with joint detection, for which the classical results do not apply, and derive a dirty-paper coding lower bound. We demonstrate that the optimal coefficient for dirty paper coding is not necessarily that of minimum mean-square error (MMSE) estimation, as in the classical setting.

Authors: Uzi Pereg

Affiliations: Technical University of Munich

Gradient-based optimization for dynamics of PEPS

We propose to optimize finite Projected Entangled Pair States (PEPS) using approximate contraction for values and gradients of appropriate cost functions. This constitutes a global optimization scheme, in contract to the established local / alternating-least-squares methods. We demonstrate the viability of the method by optimizing groundstates of the transverse field Ising model, as well as simulating the dynamics after a local quench.

Authors: Jakob Unfried (1,2), Michael Knap (1,2), Frank Pollmann (1,2), Laurens Vanderstraeten (3)

Affiliations: (1) Department of Physics, Technische Universität München, James-Franck-Straße 1, 85748 Garching, Germany (2) Munich Center for Quantum Science and Technology (MCQST), Schellingstr. 4, 80799 München, Germany (3) Department of Physics and Astronomy, University of Ghent, Krijgslaan 281, 9000 Gent, Belgium

Hybrid quantum-classical algorithms for approximate graph coloring

We present a generalization of the Quantum Approximate Optimization Algorithm (QAOA) (1) to k-dimensional qudits with k greater than 2 and show that it exhibits theoretical limitations in its performance similar to the original formulation (2) due to its locality and uniformity. In order to sidestep the locality constraint, we introduce RQAOA, a recursive version of QAOA. We then numerically evaluate the performance of level-1 RQAOA applied to the MAX-3-CUT problem to see that it typically outperforms level-1 QAOA and is in some parameter settings even competitive with the best known classical algorithms. (1) Edward Farhi, Jeffrey Goldstone, Sam Gutmann: “A Quantum Approximate Optimization Algorithm”, arXiv:1411.4028 (2) Edward Farhi, David Gamarnik, Sam Gutmann: “The Quantum Approximate Optimization Algorithm Needs to See the Whole Graph: Worst Case Examples”, arXiv:2005.08747

Authors: Sergey Bravyi (1), Alexander Kliesch (2), Robert Koenig (2), Eugene Tang (3)

Affiliations: (1) IBM Quantum, (2) TUM, (3) Caltech

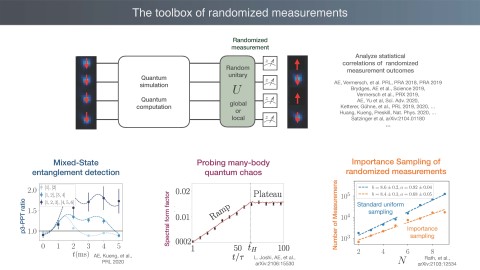
Statistical correlations of randomized measurements - A toolbox for probing synthetic quantum matter

We present statistical correlations of randomized measurements as a new toolbox to probe properties of many-body quantum states beyond standard observables. We focus on locally randomized measurements in spin models, implemented with local random unitaries. We illustrate three applications: First, we present theoretical and experimental results, obtained in a trapped ion quantum simulator, on the estimation of the 2nd Renyi entropy [1]. Secondly, we show that randomized measurement give access moments of partially transposed density matrix which allows to detect bipartite entanglement of strongly mixed quantum states [2]. Thirdly, we present a proposal to measure spectral form factors in quantum spin models which serves a unified diagnostic of many-body quantum chaos and eigenstate thermalization in closed quantum systems [3]. Lastly, we show recent results on how to improve the scaling of the required number of experimental runs using importance sampling of randomized measurements [4]. [1] Probing entanglement entropy via randomized measurements, Tiff Brydges, Andreas Elben, Petar Jurcevic, Benoît Vermersch, Christine Maier, Ben P. Lanyon, Peter Zoller, Rainer Blatt, Christian F. Roos, Science 364, 260 (2019) [2] Mixed-state entanglement from local randomized measurements, Andreas Elben, Richard Kueng, Hsin-Yuan Huang, Rick van Bijnen, Christian Kokail, Marcello Dalmonte, Pasquale Calabrese, Barbara Kraus, John Preskill, Peter Zoller, Benoît Vermersch, Phys. Rev. Lett. 125, 200501 (2020) [3] Probing many-body quantum chaos with quantum simulators, Lata Kh Joshi, Andreas Elben, Amit Vikram, Benoît Vermersch, Victor Galitski, Peter Zoller, arXiv:2106.15530 [4] Importance sampling of randomized measurements for probing entanglement, Aniket Rath, Rick van Bijnen, Andreas Elben, Peter Zoller, Benoît Vermersch, arXiv:2102.13524

Authors: (1) Center for Quantum Physics and Institute for Experimental Physics, University of Innsbruck, Austria (2) IQOQI Innsbruck, Austria (3) IQIM and Walter Burke Institute for Theoretical Physics, Caltech, Pasadena, USA (4) Univ. Grenoble Alpes, CNRS, LPMMC, Grenoble, France (5) Institute for Integrated Circuits, Johannes Kepler University Linz, Austria (6) JQI and Condensed Matter Theory Center, University of Maryland, USA (7) Department of Computing and Mathematical Sciences, Caltech, Pasadena, USA (8) ICTP and SISSA, Trieste, Italy (9) Institute for Theoretical Physics, University of Innsbruck, Austria (10) AWS Center for Quantum Computing, Pasadena, USA

Affiliations: Theory: A. Elben(1,2,3), B. Vermersch(1,2,4), R. Kueng(5), L. Joshi(1,2), A. Vikram(6), A. Rath(4), H. Huang(3,7), C. Kokail(1,2), R. van Bijnen(1,2), M. Dalmonte(8), P. Calabrese(8), B. Kraus(9), V. Galitski(6), J. Preskill(3,8,10), P. Zoller(1,2); Experiment: T. Brydges(1,2),, M. Joshi(1,2), C. Maier(1,2), P. Jurcevic(1,2), B. Lanyon(1,2), R. Blatt(1,2), C. Roos(1,2)

Electronic and transport properties of fluorinated graphene materials

In this contribution, we use a combination of electronic structure theory, transport simulations, and local current analysis to explore fluorinated graphene based transistor materials. Our efforts focus on 1D fluorinated Zigzag Graphene Nanoribbons (ZGNRs) to construct nanojunctions with atomically precise controlled fluorination degree and pattern. Electronic structure calculations within a periodic density functional theory (DFT) framework on periodic 1D structures yield information about the band structures. Performing Non-Equilibrium Green’s Function simulations on selected systems of interest, their transport properties in the quasi-stationary limit are revealed. Following a local current analysis procedure, associated electronic flux densities are mapped on a real space representation. The presence of fluorination leads to a concentration of the current in one side of the ZGNRs sheet of the spin channels, which is interesting for the potential spintronic applications.

Authors: Jingjing Shao, Beate Paulus

Affiliations: Freie Universität Berlin